Center of Mass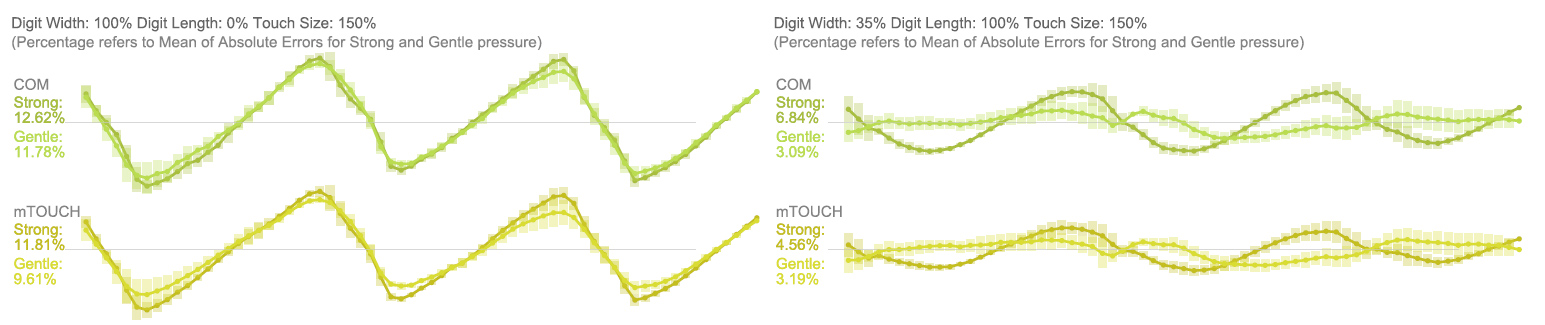
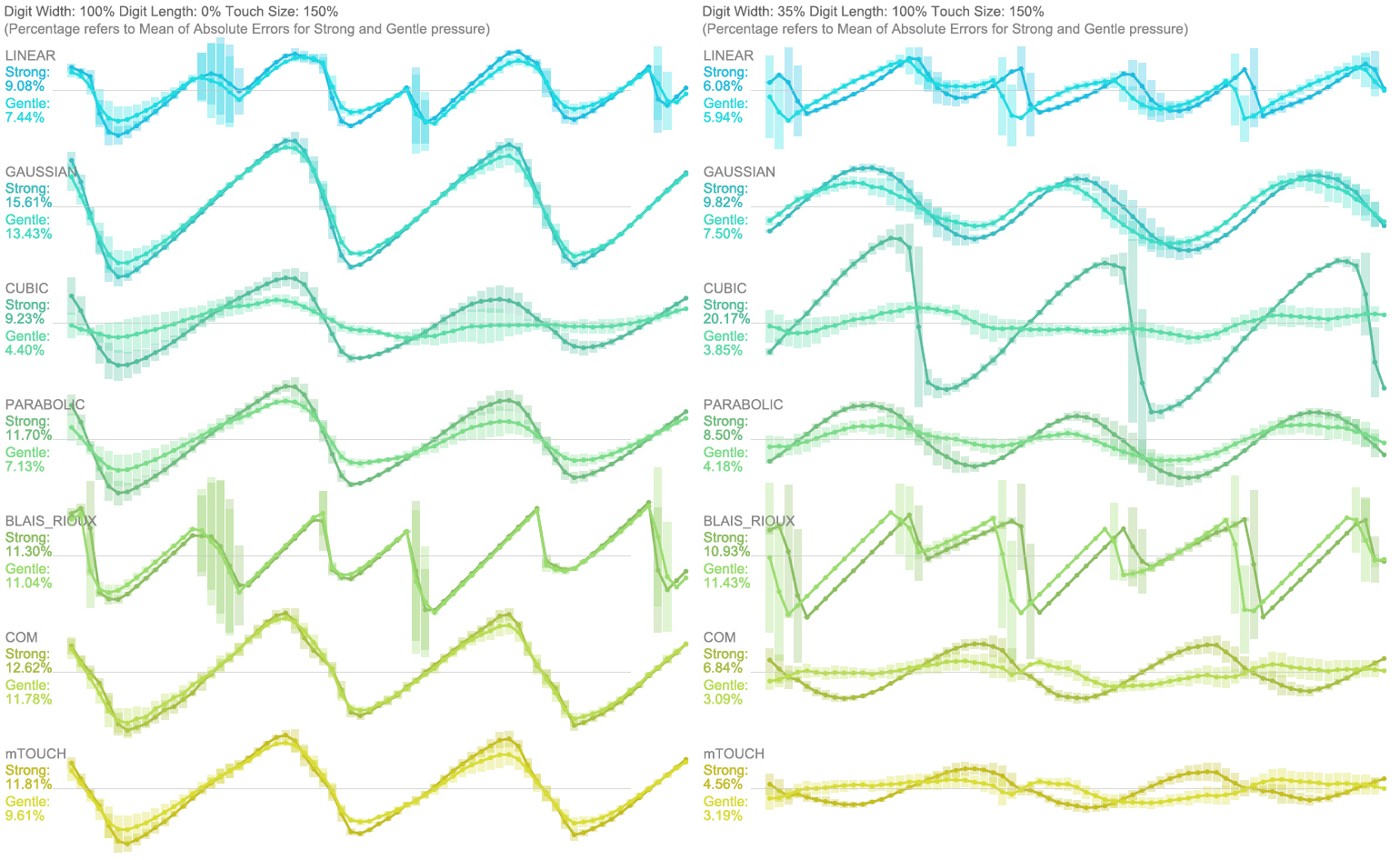
Overall Centre of Mass based approaches led to the best results, especially when using interdigitated electrodes. We used two different approaches mTOUCH calculates the touch position from the three highest values. COM uses the values of all seven electrodes.
Generally mTOUCH led to the best results, once the data had the noise-floor removed and the dynamic range mapped from 0 to 1. Anecdotally, Calculating Centre of Mass using all electrodes led to better results on the more noisy raw data.
Curve Fitting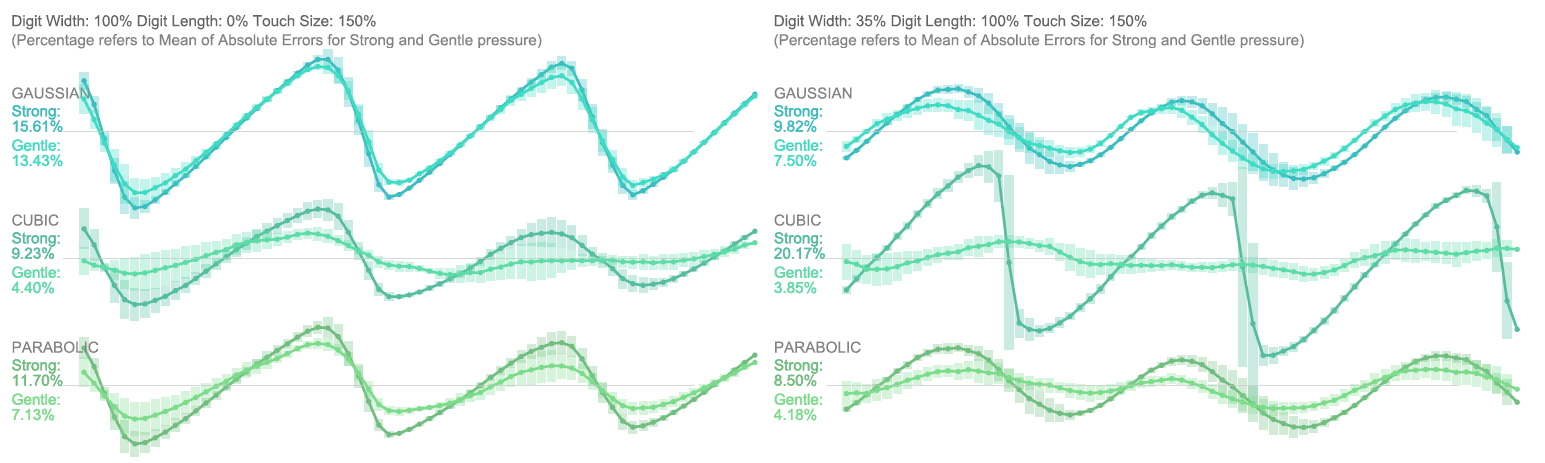
Curve Fitting methods assume that the distribution of the pressure values matches a known curve. We tested GAUSSIAN, CUBIC and PARABOLIC curves. We found that CUBIC peak-detection performed surprisingly poorly, especially for interdigitated sensors. While it performed well for low pressure levels, high pressure with CUBIC peak detection lead to some of the worst results we found.
While Centre of Mass approaches generally outperformed Curve Fitting approaches, GAUSSIAN peak-detection performed surprisingly well with regards to consistency over pressure levels and precision.
Linear Fitting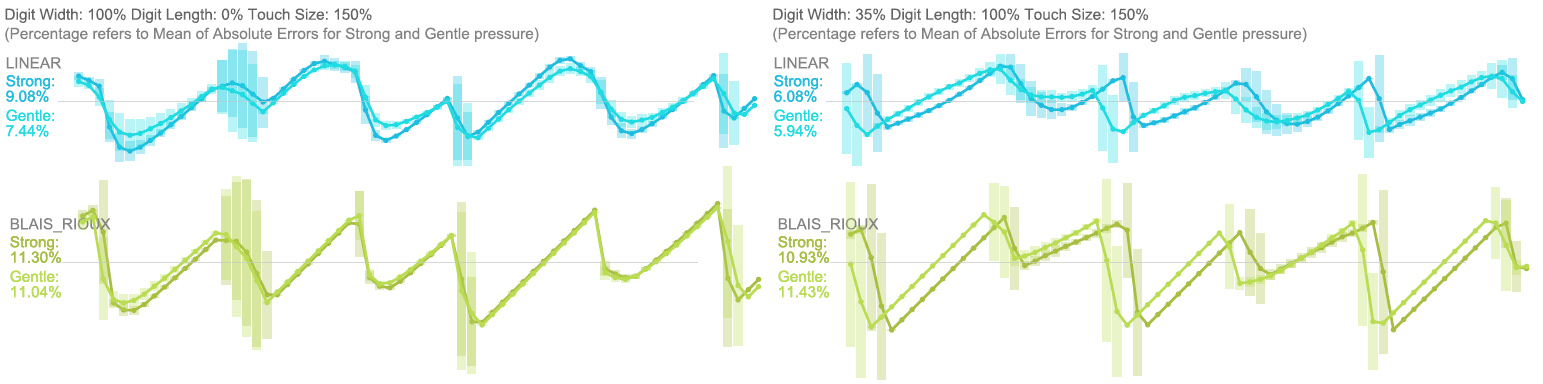
Linear Fitting follows the same logic as Curve Fitting, just that we assume that the signal has a linear propagation from its peak. Interestingly the periodic error patterns we found for these peak-detection methods had double the frequency as the others.
In general LINEAR performed well, however, the distribution of errors is slightly non-intuitive, and we speculate that a more consistent method, such as GAUSSIAN Curve Fitting might be more pleasant to users, even though the accuracy is lower. The BLAIS_RIOUX algorithm is originally designed for detecting peaks in streaming real-time data. We modified a modified version by https://link.springer.com/chapter/10.1007/978-1-4471-1921-0_28
We added a ‘naive’ approach as reference. This algorithm places the position of the finger at the centre of the electrode with the strongest response. It is somewhat of a ‘worst case’ scenario.